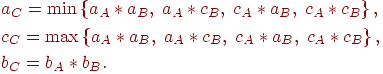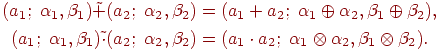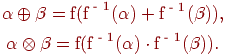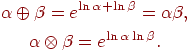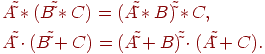| Основы теории нечетких множеств | ||||||
| 7. Лекция: Нечеткие числа и операции над
ними: версия для печати и PDA В лекции дается определение нечеткого числа, рассматриваются его свойства, описываются операции над нечеткими числами. Подробно рассматриваются нечеткие треугольные числа, а также различные арифметики нечетких треугольных чисел. | ||||||
Основные определенияНечеткое число — это нечеткое подмножество универсального множества действительных чисел, имеющее нормальную и выпуклую функцию принадлежности, то есть такую, что: а) существует значение носителя, в котором функция принадлежности равна единице, а также b) при отступлении от своего максимума влево или вправо функция принадлежности не возрастает. Нечеткое число Выпуклое нечеткое число
Подмножество
Нечеткое число Согласно принципу обобщения Заде было введено понятие
арифметических операций на множестве нечетких чисел. Для
произвольных нечетких чисел
Расширенные бинарные арифметические операции (сложение, умножение и пр.) для нечетких чисел определяются через соответствующие операции для четких чисел с использованием принципа обобщения следующим образом:
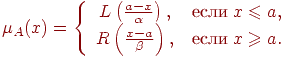
Анализ свойств арифметических операций над нечеткими числами показал, что нечеткое число не имеет противоположного и обратного чисел, сложение и умножение коммутативны, ассоциативны и в общем случае недистрибутивны. При решении задач математического моделирования нечетких систем можно использовать нечеткие числа (L-R)-типа, которые предполагают более простую интерпретацию расширенных бинарных отношений. Нечеткие числа (L-R)-типа — это разновидность нечетких чисел специального вида, т.е. задаваемых по определенным правилам с целью снижения объема вычислений при операциях над ними. Функции принадлежности нечетких чисел
(L-R)-типа задаются с помощью невозрастающих на множестве
неотрицательных действительных чисел функций действительного
переменного а) б) Очевидно, что к классу Пусть
Таким образом, при заданных Толерантное нечеткое число задается,
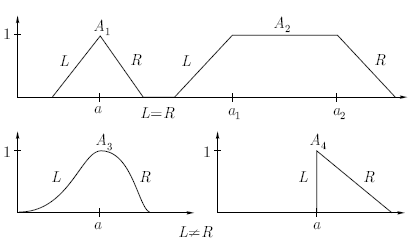
соответственно, четверкой параметров Примеры графиков функций принадлежности нечетких чисел Толерантные нечеткие числа
(L-R)-типа называют трапезоидными числами. Если мы оцениваем
параметр качественно, например, говоря: "Это значение параметра
является средним", необходимо ввести уточняющее высказывание
типа " Среднее значение — это примерно от Унимодальные нечеткие числа
(L-R)-типа называют треугольными числами. Треугольные числа формализуют высказывания типа
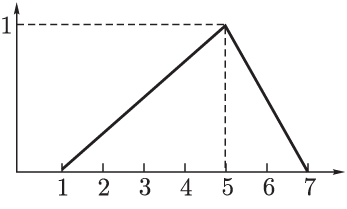
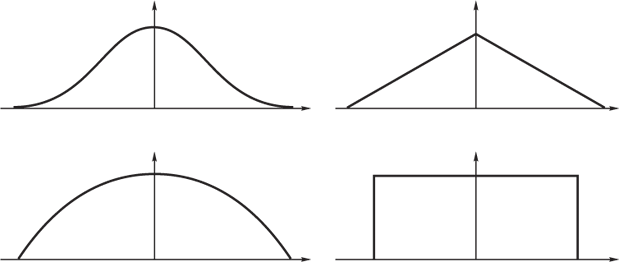
"приблизительно равно Нечеткие треугольные числа — это наиболее часто используемый тип нечетких чисел, причем чаще всего — в качестве прогнозных значений параметра. Нечеткие треугольные числаНа практике часто используется альтернативное определение нечеткого треугольного числа. Определение. Треугольным нечетким
числом
Второе число Например, на рис.
7.3 изображено нечеткое треугольное
число В общем случае при определении нечеткого
треугольного числа не обязательно использовать линейные
функции. Часто в различных приложениях используются две функции, из
которых одна монотонно возрастает на интервале Если
К сожалению, даже при ограничении нашего виденья нечетких чисел до понятия треугольных чисел, проблемы противоположного, обратного элементов и дистрибутивности остаются нерешенными. Было предложено ввести некоторые ограничения на вычисление
частных случаев вида Есть еще один существенный недостаток такого подхода. Размытость произведения зависит не только от размытости сомножителей, но и от того, какое место данные нечеткие числа занимают на числовой оси. Например, пусть
Позднее было предложено другое определение нечеткого числа. Определение. Нечетким числом
Это позволило авторам ввести понятие меры и превратить множество нечетких чисел в топологическое пространство. Далее была предложена следующая модификация определения нечеткого числа. Определение. Для любого нечеткого
числа Согласно данному определению, каждое нечеткое
число может быть представлено следующим образом: Далее вводится понятие арифметических операций над нечеткими числами такого вида. Для любых нечетких чисел
Этот подход позволяет решить проблему дистрибутивности, так как
размытость числа Несмотря на это преимущество, проблемы противоположного и обратного элементов и при таком подходе остаются нерешенными. Четкие арифметики нечетких треугольных чиселВернемся к рассмотрению нечетких треугольных чисел как частного
случая нечетких чисел Мы будем строить арифметику Определяя операции сложения и умножения, мы можем вычислять размытость суммы и произведения нечетких треугольных чисел либо по одному алгоритму, либо по разным. Сперва рассмотрим случай, когда размытость суммы и произведения нечетких треугольных чисел вычисляется по одному алгоритму. Определим операции сложения и умножения нечетких треугольных чисел следующим образом:
Опишем, какими свойствами должна обладать операция Очевидно, что для того, чтобы операция
Пусть
Для того, чтобы каждое нечеткое число
обладало противоположным, необходимо, чтобы для любого
Аналогично, если
И для любого
Легко заметить, что алгебраическая система Для того, чтобы операции
Если
Следовательно, для того, чтобы условие (2) выполнялось,
достаточно, чтобы
Нетрудно показать, что никакая группа не обладает свойством идемпотентности. Вывод Невозможно построить арифметику нечетких треугольных чисел, изоморфную арифметике действительных (четких) чисел, если размытость суммы и произведения нечетких треугольных чисел вычисляется по одному алгоритму. Теперь рассмотрим случай, когда размытость суммы и произведения определяются по разным алгоритмам. Пусть
Очевидно, что если алгебраическая система Пример. Рассмотрим поле
Таким образом, мы получим
Нетрудно убедиться, что при таком задании операций размытости
арифметика Недостатком этой арифметики является то, что в нее не входят четкие и "получеткие" числа, т.е. числа, у которых хотя бы один из коэффициентов размытости равен нулю. Но этого легко избежать, если доопределить ее, например, следующим образом:
Заметим, что, варьируя мощность изоморфного поля, мы тем самым варьируем и мощность множества коэффициентов размытости, используемых в данной арифметике. Размытые арифметики нечетких треугольных чиселВ предыдущем параграфе мы доказали, что возможно построить арифметику нечетких треугольных чисел, аналогичную арифметике четких чисел. Однако, на наш взгляд, каждая такая арифметика будет обладать одним существенным недостатком. Рассмотрим арифметику
Если Рассмотрим новый подход к арифметике нечетких чисел, который успешно формализует описанное выше свойство без потери свойств, аналогичных свойствам четкой арифметики. При этом подходе нечеткость рассуждений увеличивается, но это не всегда является минусом. Основная идея данного подхода заключается в том, что понятие нечеткости накладывается на арифметические операции. То есть результатом произведения (или сложения) двух нечетких треугольных чисел является не одно конкретное нечеткое треугольное число, а нечеткое множество, определенное на множестве нечетких треугольных чисел. Такие операции названы размытыми операциями. Следовательно, и арифметику нечетких чисел с размытыми операциями мы будем называть размытой (сокращенно РА-НТЧ). Рассмотренные выше арифметики мы будем называть четкими (сокращенно ЧА-НТЧ). Пусть нам задана некоторая ЧА-НТЧ Пусть нам даны нечеткие числа
Введем новое обозначение. Пусть
Независимо от задания арифметики На самом деле, если найдется такое число Если ЧА-НТЧ
Прежде чем говорить об ассоциативности и дистрибутивности, необходимо рассмотреть алгоритм вычисления арифметических выражений, содержащих более двух нечетких треугольных чисел. Пусть
Нетрудно убедиться, что полученная арифметика будет обладать
свойствами слабой ассоциативности и слабой дистрибутивности, т.е.
для любых
Необходимым и достаточным условием для выполнения сильных свойств
ассоциативности и дистрибутивности является условие выполнения этих
свойств в арифметике В построенной нами арифметике
И, аналогично, элемент
Нетрудно убедиться, что все нечеткие треугольные числа, мода которых равна нулю, являются нулевыми, и нечеткие треугольные числа, мода которых равна единице, являются единичными. Вернемся теперь к рассмотрению проблемы, описанной в начале
данного параграфа. Пусть число
Проблема противоположного и обратного элементов решается по
аналогии с проблемой коммутативности; в слабом варианте проблема
решается автоматически, а усиленный вариант зависит от того,
существуют ли противоположный и обратный элементы в арифметике | ||||||
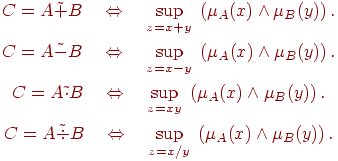
![\mu _A (x) = \left\{ {\begin{array}{*{20}c}
{\frac{{x - a}}
{{b - a}},} & {\t{\char229}\t{\char241}\t{\char235}\t{\char232}\;x \in
[a,b],} & {} \\
{\frac{{x - c}}
{{b - c}},} & {\t{\char229}\t{\char241}\t{\char235}\t{\char232}\;x \in
[b,c],} & {} \\
{0,} & {\t{\char226}{\kern 1pt}
\;\t{\char239}\t{\char240}\t{\char238}\t{\char242}\t{\char232}\t{\char226}\t{\char237}\t{\char238}\t{\char236}\;\t{\char241}\t{\char235}\t{\char243}\t{\char247}\t{\char224}\t{\char229}.} & {} \\
\end{array} } \right.](7.files/209245c0b24b64b624c454a0aea7d823.png)