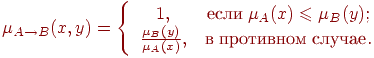| Основы теории нечетких множеств |
| 10. Лекция: Теория приближенных рассуждений:
версия для печати и PDA В лекции рассматривается композиционное правило вывода — главное понятие теории приближенных рассуждений. Описывается работа нечеткой экспертной системы, основанной на принципах теории приближенных вычислений. |
|
Под приближенными рассуждениями понимается процесс, при котором из нечетких посылок получают некоторые следствия, возможно, тоже нечеткие. Приближенные рассуждения лежат в основе способности человека понимать естественный язык, разбирать почерк, играть в игры, требующие умственных усилий, в общем, принимать решения в сложной и не полностью определенной среде. Эта способность рассуждений в качественных, неточных терминах отличает интеллект человека от интеллекта вычислительной машины. Основным правилом вывода в традиционной логике является правило
modus ponens, согласно которому мы судим об истинности высказывания
Во многих привычных рассуждениях, однако, правило modus ponens
используется не в точной, а в приближенной форме. Так, обычно мы
знаем, что Далее мы обсудим способ формализации приближенных рассуждений, основанный на понятиях, введенных нами на предыдущей лекции. Однако, в отличие от традиционной логики, нашим главным инструментом будет не правило modus ponens, а так называемое композиционное правило вывода, весьма частным случаем которого является правило modus ponens. Композиционное правило выводаКомпозиционное правило вывода — это
всего лишь обобщение следующей знакомой процедуры. Предположим, что
имеется кривая Обобщим теперь этот процесс, предположив, что
Чтобы продвинуться еще на один шаг по пути обобщения,
предположим, что Правило. Пусть
Пример. Пусть A = МАЛЫЙ
Тогда получим
B = БОЛЕЕ ИЛИ МЕНЕЕ МАЛЫЙ, если терм БОЛЕЕ ИЛИ МЕНЕЕ определяется как оператор увеличения нечеткости. Словами этот приближенный вывод можно записать в виде
Правило modus ponens как частный случай композиционного правила выводаКак мы увидим ниже, правило modus ponens можно рассматривать как частный случай композиционного правила вывода. Чтобы установить эту связь, мы сперва обобщим понятие материальной импликации с пропозициональными переменными на нечеткие множества. Пусть
Тогда
Однако, это не единственное обобщение оператора импликации. В следующей таблице показаны различные интерпретации этого понятия. Определим теперь обобщенное правило modus ponens (generalized modus ponens). Приведенная формулировка имеет два отличия от традиционной
формулировки правила modus ponens : во-первых, здесь допускается,
что Нечеткие экспертные системыЛогико-лингвистические методы описания систем основаны на том, что поведение исследуемой системы описывается в естественном (или близком к естественному) языке в терминах лингвистических переменных. Входные и выходные параметры системы рассматриваются как лингвистические переменные, а качественное описание процесса задается совокупностью высказываний следующего вида: L1 если A11 и/или A2 и/или ... и/или A1m, то B11 и/или ... и/или B1n, L2 если A21 и/или A22 и/или ... и/или A2m, то B21 и/или ... и/или B2n, ..................... Lk если Ak1 и/или Ak2 и/или ... и/или Akm, то Bk1 и/или ... и/или Bkn, где Подобные вычисления составляют основу нечетких экспертных систем. Каждая нечеткая экспертная система использует нечеткие утверждения и правила. Затем с помощью операторов вычисления дизъюнкции и конъюнкции описание системы можно привести к виду L1: если А1, то B1, L2: если А2, то B2, ..................... Lk: если Аk, то Bk, где В основе построения логико-лингвистических систем лежит рассмотренное выше композиционное правило вывода Заде. Преимущество данной модели - в ее универсальности. Нам неважно,
что именно на входе — конкретные числовые значения или некоторая
неопределенность, описываемая нечетким множеством. Но за данную
универсальность приходится расплачиваться сложностью системы — нам
приходится работать в пространстве размерности Нечетким логическим выводом (fuzzy logic inference)
называется аппроксимация зависимости В общем случае нечеткий вывод решения происходит за три (или четыре) шага: 1) этап фаззификации. С помощью функций принадлежности
всех термов входных лингвистических переменных и на основании
задаваемых четких значений из универсумов входных лингвистических
переменных определяются степени уверенности в том, что выходная
лингвистическая переменная принимает конкретное значение. Эта
степень уверенности есть ордината точки пересечения графика функции
принадлежности терма и прямой 2) этап непосредственного нечеткого вывода. На основании набора правил — нечеткой базы знаний — вычисляется значение истинности для предпосылки каждого правила на основании конкретных нечетких операций, соответствующих конъюнкции или дизъюнкции термов в левой части правил. В большинстве случаев это либо максимум, либо минимум из степеней уверенности термов, вычисленных на этапе фаззификации, который применяется к заключению каждого правила. Используя один из способов построения нечеткой импликации, мы получим нечеткую переменную, соответствующую вычисленному значению степени уверенности в левой части правила и нечеткому множеству в правой части правила. Обычно в качестве вывода используется минимизация или правила продукции. При минимизирующем логическом выводе выходная функция принадлежности ограничена сверху в соответствии с вычисленной степенью истинности посылки правила (нечеткое логическое И). В логическом выводе с использованием продукции выходная функция принадлежности масштабируется с помощью вычисленной степени истинности предпосылки правила. 3) этап композиции (агрегации, аккумуляции). Все нечеткие множества, назначенные для каждого терма каждой выходной лингвистической переменной, объединяются вместе, и формируется единственное нечеткое множество — значение для каждой выводимой лингвистической переменной. Обычно используются функции MAX или SUM. 4) этап дефаззификации (необязательный). Используется тогда, когда полезно преобразовать нечеткий набор значений выводимых лингвистических переменных к точным. Имеется достаточно большое количество методов перехода к точным значениям (по крайней мере, 30). Два примера общих методов — "методы полной интерпретации" и "по максимуму". В методе полной интерпретации точное значение выводимой переменной вычисляется как значение "центра тяжести" функции принадлежности для нечеткого значения. В методе максимума в качестве точного значения выводимой переменной принимается максимальное значение функции принадлежности. В теории нечетких множеств процедура дефаззификации аналогична нахождению характеристик положения (математического ожидания, моды, медианы) случайных величин в теории вероятности. Простейшим способом выполнения процедуры дефаззификации является выбор четкого числа, соответствующего максимуму функции принадлежности. Однако пригодность этого способа распространяется лишь на одноэкстремальные функции принадлежности. Для многоэкстремальных функций принадлежности часто используются следующие методы дефаззификации: 1) COG (Center Of Gravity) — "центр тяжести". Физическим аналогом этой формулы является нахождение центра тяжести плоской фигуры, ограниченной осями координат и графиком функции принадлежности нечеткого множества. 2) MOM (Mean Of Maximums) — "центр максимумов". При использовании метода центра максимумов требуется найти среднее арифметическое элементов универсального множества, имеющих максимальные степени принадлежностей. 3) First Maximum — "первый максимум" — максимум функции принадлежности с наименьшей абсциссой. Функциональная схема процесса нечеткого вывода в упрощенном виде представлена на рис. 10.2. На этой схеме выполнение первого этапа нечеткого вывода — фаззификации — осуществляет фаззификатор. За процедуру непосредственно нечеткого вывода ответственна машина нечеткого логического вывода, которая производит второй этап процесса вывода на основании задаваемой нечеткой базы знаний (набора правил), а также этап композиции. Дефаззификатор выполняет последний этап нечеткого вывода — дефаззификацию.
Рассмотрим алгоритм нечеткого вывода на конкретном примере. Пусть у нас есть некоторая система, например, реактор, описываемая тремя параметрами: температура, давление и расход рабочего вещества. Все показатели измеримы, и множество возможных значений известно. Также из опыта работы с системой известны некоторые правила, связывающие значения этих параметров. Предположим, что сломался датчик, измеряющий значение одного из параметров системы, но знать его показания необходимо хотя бы приблизительно. Тогда встает задача об отыскании этого неизвестного значения (пусть это будет давление) при известных показателях двух других параметров (температуры и расхода) и связи этих величин в виде следующих правил:
В нашем случае Температура, Давление и Расход — лингвистические переменные. Опишем каждую из них. Температура. Универсум (множество возможных значений) —
отрезок
Давление. Универсум — отрезок
Расход. Универсум — отрезок
Пусть известны значения Температура 85 и Расход 3,5 . Произведем расчет значения давления. Последовательно рассмотрим этапы нечеткого вывода: Сначала по заданным значениям входных параметров найдем степени
уверенности простейших утверждений вида "Лингв. переменная
Затем вычислим степени уверенности посылок правил:
Следует отметить также тот факт, что с помощью преобразований нечетких множеств любое правило, содержащее в левой части как конъюнкции, так и дизъюнкции, можно привести к системе правил, в левой части каждого будут либо только конъюнкции, либо только дизъюнкции. Таким образом, не уменьшая общности, можно рассматривать правила, содержащие в левой части либо только конъюнкции, либо только дизъюнкции. Каждое из правил представляет из себя нечеткую импликацию. Степень уверенности посылки мы вычислили, а степень уверенности заключения задается функцией принадлежности соответствующего терма. Поэтому, используя один из способов построения нечеткой импликации, мы получим новую нечеткую переменную, соответствующую степени уверенности в значении выходных данных при применении к заданным входным соответствующего правила. Используя определение нечеткой импликации как минимума левой и правой частей (определение Mamdani), имеем:
Теперь необходимо объединить результаты применения всех правил. Этот этап называется аккумуляцией. Один из основных способов аккумуляции — построение максимума полученных функций принадлежности. Получаем:
Полученную функцию принадлежности уже можно считать результатом. Это новый терм выходной переменной Давление. Его функция принадлежности говорит о степени уверенности в значении давления при заданных значениях входных параметров и использовании правил, определяющих соотношение входных и выходных переменных. Но обычно все-таки необходимо какое-то конкретное числовое значение. Для его получения используется этап дефаззификации, т.е. получения конкретного значения из универса по заданной на нем функции принадлежности. Существует множество методов дефаззификации, но в нашем случае достаточно метода первого максимума. Применяя его к полученной функции принадлежности, получаем, что значение давления — 50. Таким образом, если мы знаем, что температура равна 85, а расход рабочего вещества — 3,5, то можем сделать вывод, что давление в реакторе равно примерно 50. |

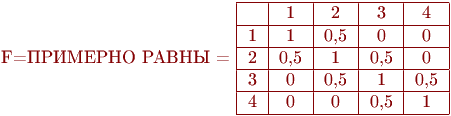
![B = [1\quad 0,6\quad 0,2\quad 0] \circ \left[
{\begin{array}{*{20}c}
1 & {0,5} & 0 & 0 \\
{0,5} & 1 & {0,5} & 0 \\
0 & {0,5} & 1 & {0,5} \\
0 & 0 & {0,5} & 1 \\
\end{array} } \right] = [1\quad 0,6\quad 0,5{\kern 1pt} {\kern 1pt} \quad
0,2],](10.files/93ddb2af34601aac9934a4459245e6e0.png)